thuvientoan.net xin gửi đến bạn đọc Đề thi vào lớp 10 chuyên Toán Sở Giáo dục và Đào tạo Bà Rịa - Vũng Tàu năm 2020
Sáng ngày 18/7/2020, các thí sinh dự thi vào lớp chuyên Toán trường THPT chuyên Lê Quý Đôn - Tỉnh Bà Rịa Vũng Tàu bắt đầu làm bài môn Toán chuyên.
Đề thi gồm 5 câu với thời gian làm bài 150 phút, mỗi câu gồm nhiều ý nhỏ xoay quanh các chủ đề Phương trình, Hệ phương trình, Bất đẳng thức, Phương trình nghiệm nguyên, Hình học,...
Do tình hình dịch bệnh nên đề thi năm nay có phần nhẹ hơn các năm trước, tập trung chủ yếu vào chương trình Nâng cao và chuyên Toán THCS, đòi hỏi thí sinh phải có nền tảng kiến thức và khả năng tư duy sáng tạo.
Điểm nhấn của đề thi năm nay là hai câu Bất đẳng thức, Cực trị nằm ở câu 3 và câu 5 của đề thi cũng là hai câu phân loại nhằm đánh giá các học sinh giỏi, có năng khiếu về Toán.
Bên cạnh gửi đến bạn đọc đề thi, đội ngủ giáo viên của thuvientoan.net còn biên soạn lời giải chi tiết để các bạn có một nguồn tư liệu học tập.
Hi vọng các bạn sẽ học tập được những điều bổ ích mà tài liệu này mang lại. Chúc các bạn học tốt!
Trích dẫn:
Câu 1. (3,0 điểm)
b) Giải phương trình: căn bậc hai (x^2 + 3) = x + căn bậc hai (2x - 1)
c) Giải hệ phương trình: x - y + 2 = xy và (2 - x)y = x^2 + y^2.
Câu 2. (2,0 điểm)
a) Cho đa thức P(x) = (x - 2)(x^2 + ax - 8) + bx^2 với a, b là các số thực thỏa mãn a + b < 1. Chứng minh rằng phương trình P(x) = 0 có bốn nghiệm phân biệt.
c) Tìm tất cả các cặp số nguyên (x,y) thỏa mãn x(x + y)^2 - y + 1 =0.
Câu 4. (3,0 điểm)
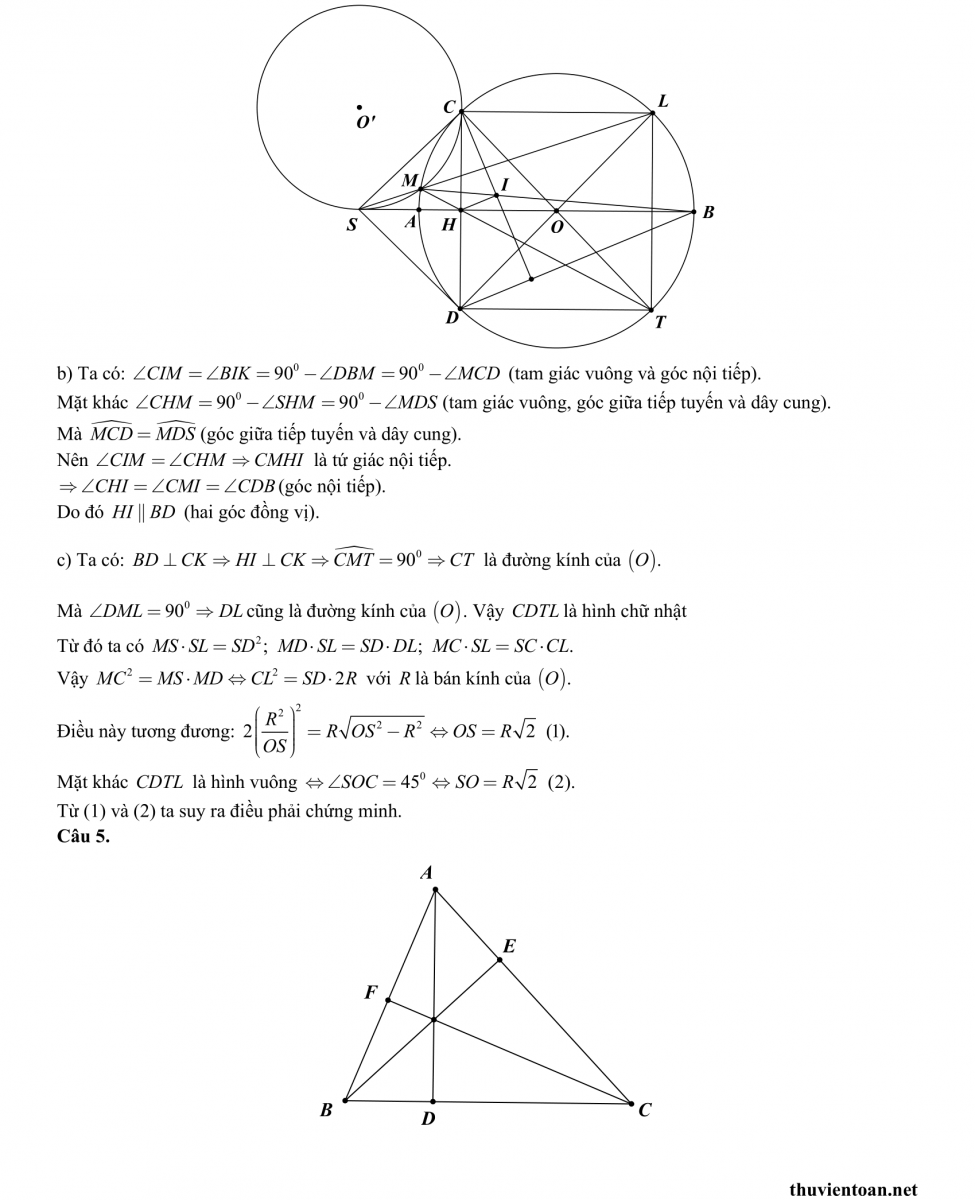
Cho đường tròn (O) đường kính AB. Từ điểm S thuộc tia đối của tia AB kẻ đến (O) hai tiếp tuyến SC, SD (C và D là hai tiếp điểm). Gọi H là giao điểm của đường kính AB và dây CD. Vẽ đường tròn (O') đi qua C và tiếp xúc với đường thẳng AB tại S. Hai đường tròn (O) và (O') cắt nhau tại điểm M khác C.
a) Chứng minh tứ giác SMHD nội tiếp.
b) Gọi K là hình chiếu vuông góc của C trên BD, I là giao điểm của BM và CK. Chứng minh HI song song với BD.
c) Các đường thẳng SM và HM lần lượt cắt (O) tại các điểm L và T (L, T khác M). Chứng minh rằng tứ giác CDTL là hình vuông khi và chỉ khi MC^2 = MS.MD.
Câu 5. (1,0 điểm)
Cho tam giác ABC có ba góc nhọn và có trực tâm H. Gọi D, E, F lần lượt là chân ba đường cao kẻ từ A, B, C của tam giác ABC. Biết (AB/HF)^2 + (AC/HE)^2 + (BC/HD)^2 = 36. Hãy chứng minh rằng tam giác ABC đều.



 TẢI FILE PDF: Tại đây.
TẢI FILE PDF: Tại đây.
THEO THUVIENTOAN.NET



